本日のスライド
PCの場合、「スライド表示」を別タブで表示して画面の左右に記事とスライドを表示しながら見ることをお勧めします。
スマホの場合は、スライドを一通り読んでから記事を読むと理解がしやすいかと思います。
スライドはpdfでダウンロードできますので商用利用目的を除いてご自由にご使用ください。
2進数の負数表現(P.1 ~ P. 7)
2進数による負数(マイナスの数値)の表現方法を説明します。下記の3つが主な方法になります。
- 符号+絶対値
- 1の補数表現
- 2の補数表現
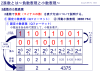
符号と絶対値(P. 1)
MSBの1bitで符号を表して、残りのbitで数値の絶対値を表現する方法です。
MSBが0の場合⇒正
MSBが1の場合⇒負
の数値となります。
例えば、「ー39」を8bitで表す場合、0b10100111となる。
1の補数(P. 2)
MSBの1bit符号を表して、絶対値の2進数に対する負数を各桁bit反転したものとする表現方法。
例えば、「-39」を8bitの1の補数で表す場合、
- 絶対値である「39」の2進数表現を行う。
- 「39」の2進数表現は0b00100111
- 各桁をbit反転させる0b11011000。これが1の補数の「-39」を表す。
1の補数は、MSBを除いて各bitに対して重みを乗じて数値を求める際に、負論理*にて導出する。
*負論理とは:正論理の逆。0をアクティブ、1をネガティブと考える方式。
2の補数(P. 3)
1の補数に、+1を加えて負数を表現する方法。
一般的に広く負数の表現方法として採用されている。
例えば、「-39」を8bitの1の補数で表す場合、
- 絶対値である「39」の2進数表現を行う。
- 「39」の2進数表現は0b00100111
- 各桁をbit反転させる0b11011000。これが1の補数となる
ここまでが上記と同じ - +1を加えて、0b11011001。これが2の補数で、「-39」を表す。
補数とは(P. 4)
補数とは、「ある数値」を「決められた数値」へと変換するために補う数値のことです。
N進数m桁の「ある数値」に対する「N-1の補数」は
「加算することでm桁のN進数の符号なし整数で表すことができる最大の値に変換する」役割を持ちます。
例として、2進数8桁の「0b01111110」に対する「1の補数」は、
「0b10000001」となり、加算すると「0b11111111」となり、2進数8桁の符号なし整数で表すことができる最大の値となります。
N進数m桁の「ある数値」に対する「Nの補数」は
「加算することで桁上がりが起き、m桁のN進数の符号なし整数で表すことができる最小の値(=0)に変換する」役割を持ちます。
例として、2進数8桁の「0b01111110」に対する「2の補数」は、
「0b10000010」となり、加算すると「0b100000000」となり、2進数8桁の符号なし整数で表すと「0b00000000」となり、最小の値となります。
各表現方法の比較(P. 5 ~ P. 6)
各負数の表現方法について、①数値表現と②加減算について比較する。
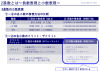
数値表現について
「符号と絶対値」の場合(8bit)「1の補数」の場合(8bit)
- 0の表現において「+0」と「-0」があり、重複が起きている
- -128の最小値を表現することができない
「2の補数」の場合(8bit)
- 0の重複がない
- -128の最小値を表現することができる
加減算について
加算について
「符号と絶対値」、「1の補数」、「2の補数」いづれにおいても同様の結果を得ることができる。
減算について
「符号と絶対値」、「1の補数」では減算の後に変換処理が必要となる
「2の補数」では、変換処理が不要である。
上記より、負数を表す場合は2の補数が最も多く用いられる。
2進数の小数表現(P. 7~P. 14)
2進数で小数を表現する方法を説明します。下記の2つが主な手法になります。
- 固定小数表現(Qフォーマット)
- 浮動小数表現(IEEE 754)
固定小数(Qフォーマット)
固定小数とは、その名の通り小数点の位置を固定して2進数の小数を表現する方式である。
小数点以下のbitの重みは、LSBに1bit進むごとに、2の指数部を-1ずつしていく。
つまり、小数は\(\frac{1}{2^n}\)の組み合わせで表現することになる。
Qフォーマットの表現について(P. 7~P. 8)
代表的な固定小数の表現として、Qフォーマットと呼ばれるものがある。
Qフォーマットの数値の表し方は、数値が8bit幅で小数点以下が4bitの場合
Q4.4
と表される。
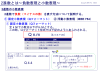
実数からQフォーマットへの変換 (P.9)
実数「-3.145」をQ4.4形式へ変換する方法について、解説をする。
- -3.145を\(2^4\)を乗する。結果は、-50.32となる
- 整数部分を8bit幅の2進数2の補数表現で表現する
- ②で表現した2進数にQ4.4の示す位置に小数点を置く
※数値や小数点以下のbit幅によっては、誤差が生じる可能性がある。
浮動小数(IEE 754)(P. 10~P. 13)
浮動小数とは、数値によって小数点の位置が可変で定まっていない小数表現である。
IEEE754
IEEE 754の規格では、浮動小数の表現方式が記載されている。
\[\pm (f)_2 \times 2^e\]
2進数を浮動小数(IEEE 754)(単精度32bit)に変換する
- 整数部を1にする正規化を行い、上記の形式で表現する。
- ①の数値を32bitで割り当てられた領域(符号部、指数部、仮数部)に表現する。
- 仮数部については、①の実際の数値から+127のバイアスをかけた数値を2進数8bitで表す
- 仮数部については、①の整数の1を切り捨てて、小数以下の部分を抽出する
実数を浮動小数(IEEE 754)(単精度32bit)に変換する
例として、-3.125を単精度浮動小数表現に変換する。
- 符号部を決定する。負の数値より、符号部が1になる。
- 絶対値を取る。3.125となる。
- 固定小数表現に変換する。(通常、小数以下の桁数を大きくとるがここでは簡単のために、Q4.4とする)
- 正規化を行い、整数部を1にする。
- ④の正規化した数値を32bitで割り当てられた領域に表現する
各表現方法の比較
P. 14に各数値の表現について、固定小数と浮動小数表現で行った場合を比較している。
固定小数と浮動小数のメリットデメリットについて
固定小数
メリット:使用メモリを必要最低限にすることができる。処理が高速
デメリット:表現できる数値範囲が狭い。自由度が低く、使い勝手が悪い
浮動小数
メリット:表現できる数値範囲が広い。自由度が高く数値に合わせて表現できる
デメリット:不要なメモリ領域も確保される。処理が固定小数と比較して低速
上記のようなメリットデメリットがあるが、一般的には自由度の高さから浮動小数表現が使用される場合が多い
まとめ
今回の記事では、2進数での負数の表し方と小数の表し方について説明した。
- 負数の表現には、①符号と絶対値、②1の補数、③2の補数の3種類が主にある
- 負数表現については、数値の表現範囲や計算のしやすさから③の2の補数が一般的に広く使用される
- 小数の表現には、①固定小数と②浮動小数の2種類が主にある。
- 小数表現については、自由度の高さから一般的に浮動小数表現が広く使用されている。
- 各表現方法について、実数からの変換方法について説明をした。